Standardization and the parametric g-formula
What If: Chapter 13
Elena Dudukina
2021-05-27
1 / 17
13.1 Standardization as an alternative to IP weighting
- Average treatment effect (ATE), or average causal effect (ACE) of smoking cessation on weight gain
- Causal contrast to assess: \(E[Y^{a=1, c=0}] - E[Y^{a=0, c=0}]\)
- Marginal weight gain difference had everyone stopped smoking vs had no one stopped smoking (everyone was treated vs everyone was untreated)
- Ignoring loss-to-follow-up from 1971 (baseline) through 1982
- Ignoring time-varying nature of the treatment and potential time-varying confounding
- Assuming conditional exchangeability based on age, sex, race, education, smoking intensity and duration, physical activity, exercise, and baseline weight
2 / 17
13.1 Standardization as an alternative to IP weighting
- Same causal question
- G-formula for ATE estimation
- NHEFS data from 1629 cigarette smokers aged 25-74 years who had a baseline visit and a follow-up visit
- Assumptions recap in the presentation for Chapter 12
3 / 17
library(tidyverse)library(magrittr)# getting the datadata <- readr::read_csv(file = "https://cdn1.sph.harvard.edu/wp-content/uploads/sites/1268/1268/20/nhefs.csv") %>% mutate( education = case_when( education == 1 ~ "8th grade or less", education == 2 ~ "HS dropout", education == 3 ~ "HS", education == 4 ~ "College dropout", education == 5 ~ "College or more", T ~ "missing" ) ) %>% mutate(across(.cols = c(sex, race, education, exercise, active), .fns = forcats::as_factor)) %>% drop_na(qsmk, sex, race, education, exercise, active, wt82)# what's inside?data %>% select(qsmk, age, sex, race, education, wt71, smokeintensity, smokeyrs, exercise, active)## # A tibble: 1,566 x 10## qsmk age sex race education wt71 smokeintensity smokeyrs exercise## <dbl> <dbl> <fct> <fct> <fct> <dbl> <dbl> <dbl> <fct> ## 1 0 42 0 1 8th grade or … 79.0 30 29 2 ## 2 0 36 0 0 HS dropout 58.6 20 24 0 ## 3 0 56 1 1 HS dropout 56.8 20 26 2 ## 4 0 68 0 1 8th grade or … 59.4 3 53 2 ## 5 0 40 0 0 HS dropout 87.1 20 19 1 ## 6 0 43 1 1 HS dropout 99 10 21 1 ## 7 0 56 1 0 HS 63.0 20 39 1 ## 8 0 29 1 0 HS 58.7 2 9 2 ## 9 0 51 0 0 HS dropout 64.9 25 37 2 ## 10 0 43 0 0 HS dropout 62.3 20 25 2 ## # … with 1,556 more rows, and 1 more variable: active <fct>| Characteristics | Smokers | Non-smokers |
|---|---|---|
| age | 46.2 (12.2) | 42.8 (11.8) |
| sex | 183 (45.4%) | 621 (53.4%) |
| race | 36 (8.9%) | 170 (14.6%) |
| College or more | 62 (15.4%) | 115 (9.9%) |
| wt71 | 72.4 (15.6) | 70.3 (15.2) |
| smokeintensity | 18.6 (12.4) | 21.2 (11.5) |
| smokeyrs | 26.0 (12.7) | 24.1 (11.7) |
| exercise | 164 (40.7%) | 441 (37.9%) |
| active | 45 (11.2%) | 104 (8.9%) |
4 / 17
13.1 Standardization as an alternative to IP weighting
- \(\hat{E}[Y|A=1]\) - \(\hat{E}[Y|A=0]\)
- Does not have a causal interpretation because exchangeability does not hold
- Quitters and non-quitters are different in respect to characteristics affecting weight gain
lm(data = data, formula = wt82_71 ~ qsmk) %>% broom::tidy(., conf.int = T) %>% select(term, conf.low, estimate, conf.high)## # A tibble: 2 x 4## term conf.low estimate conf.high## <chr> <dbl> <dbl> <dbl>## 1 (Intercept) 1.54 1.98 2.43## 2 qsmk 1.66 2.54 3.435 / 17
13.1 Standardization as an alternative to IP weighting
Assume
- Exchangeability: \(Y^{a}\perp\perp\ A\)
- Treated individuals (A=1) had they been untreated (A=0) had the same probability of the potential outcome (PO)
- Conditional exchangeability: \(Y^{a}\perp\perp\ A|L\), where L closes all back-door paths between A and Y
- When accounted for all variables in L, treated individuals (A=1) had they been untreated (A=0) had the same probability of the potential outcome
- Treated individuals (A=1) had they been untreated (A=0) had the same probability of the potential outcome (PO)
- Positivity
- Positive probability of observing each level of treatment in each strata of L
- \(Pr(A=a|L=l > 0)\) for all \(a\) and \(l\)
- Consistency
- We observe PO - the one under actually received treatment
- \(Pr[Y^{a=1}|A=1] = Pr[Y=1|A=1]\)
- Well-defined intervention ➡️ well-defined (de)confounding
- No model misspesification
6 / 17
13.1 Standardization as an alternative to IP weighting
- Adjustment (standardization) formula
- \(\Sigma_lE[Y|A=a, L=l]Pr[L=l]\)
- if conditional exchangeability holds given L
- in this example we also condition on C=0: \(\Sigma_lE[Y|A=a, C=0, L=l]Pr[L=l]\)
- To compute the standardized mean outcome in the uncensored treated, we need to compute the mean outcomes in the uncensored treated in each stratum \(l\) of the confounders \(L\)
- \(E[Y|A=1, C=0, L=l]\)
7 / 17
13.2 Estimating the mean outcome via modeling
- High-dimensional data with few observation ➡️ nonparametric modeling is not going to work
- Parametric model:
- \(\hat{E}[Y|A=a, C=0, L=l]Pr[L=l]\)
8 / 17
13.3 Standardizing the mean outcome to the confounder distribution
n <- nrow(data)fit_qsmk <- glm(data = data, qsmk ~ 1, family = binomial())p_qsmk <- predict(fit_qsmk, type = "response")p_qsmk <- p_qsmk[[1]]# fit a regression of the outcome on the exposure and confoundersQ <- glm(data = data, formula = wt82_71 ~ qsmk + sex + race + age + I(age*age) + education + smokeintensity + I(smokeintensity*smokeintensity) + smokeyrs + I(smokeyrs*smokeyrs) + exercise + active + wt71 + I(wt71*wt71), family = gaussian())# create predicted Y_a for all observationsdata %<>% mutate( new_qsmk = rbinom(n = n, size = 1, prob = p_qsmk))data %<>% mutate( wt82_71_pred = predict(Q, type = "response"))# generate data sets where a is set to 0 and 1data_qsmk0 <- data %>% mutate(qsmk = 0) data_qsmk1 <- data %>% mutate(qsmk = 1)9 / 17
# compute PO for all observations, sets qsmk=0data_qsmk0 %<>% mutate( wt82_71_po = predict(Q, newdata = data_qsmk0, type = "response"))# compute PO for all observations, sets qsmk=1data_qsmk1 %<>% mutate( wt82_71_po = predict(Q, newdata = data_qsmk1, type = "response"))data_new <- bind_rows(data_qsmk0, data_qsmk1)glm(wt82_71_po ~ qsmk, family = gaussian(link = "identity"), data = data_new) %>% broom::tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.75 0.0718 24.3 6.89e-120## 2 qsmk 3.46 0.102 34.1 6.41e-21710 / 17
library(tidymodels)set.seed(972188635)boots <- bootstraps(data, times = 1e3, apparent = FALSE)gform <- function(data) { glm(formula = wt82_71~qsmk + sex + race + age + I(age*age) + education + smokeintensity + I(smokeintensity*smokeintensity) + smokeyrs + I(smokeyrs*smokeyrs) + exercise + active + wt71 + I(wt71*wt71), family = gaussian(), data = data)}p_qsmk <- glm(data = data, qsmk~1, family = binomial())qsmk_pred <- predict(p_qsmk, type = "response")n <- nrow(data)qsmk_pred <- qsmk_pred[[1]]boot_models <- boots %>% mutate( model = map(.x = splits, ~gform(data = .x)), splits = map(splits, ~ as_tibble(.x)), # simulate qsmk with observed frequency as if it was randomized splits = map(splits, ~mutate(.x, qsmk = rbinom(n = n, size = 1, prob = qsmk_pred))), # simulate P.O.s splits = map(splits, ~mutate(.x, po = rnorm(n = n, mean = predict(Q, newdata = .x), sd = predict(Q, newdata = .x, se.fit = T)$se.fit))), gform = map(splits, ~glm(po ~ qsmk, family = gaussian(link = "identity"), data = .x)), gform_tidy = map(gform, ~broom::tidy(.x)) )11 / 17
# percentile method for 95% CIpct_res <- boot_models %>% select(id, gform_tidy) %>% bind_rows(.id = "boot") %>% unnest(cols = c(gform_tidy)) %>% filter(term == "qsmk")12 / 17
13.3 Standardizing the mean outcome to the confounder distribution
p <- pct_res %>% ggplot(aes(x = estimate)) + geom_histogram(bins = 100) + theme_light() + theme_minimal() + geom_vline(aes(xintercept = quantile(estimate, probs = 0.5)), color = "cyan") + geom_vline(aes(xintercept = quantile(estimate, probs = 0.025)), color = "lightblue") + geom_vline(aes(xintercept = quantile(estimate, probs = 0.975)), color = "lightblue")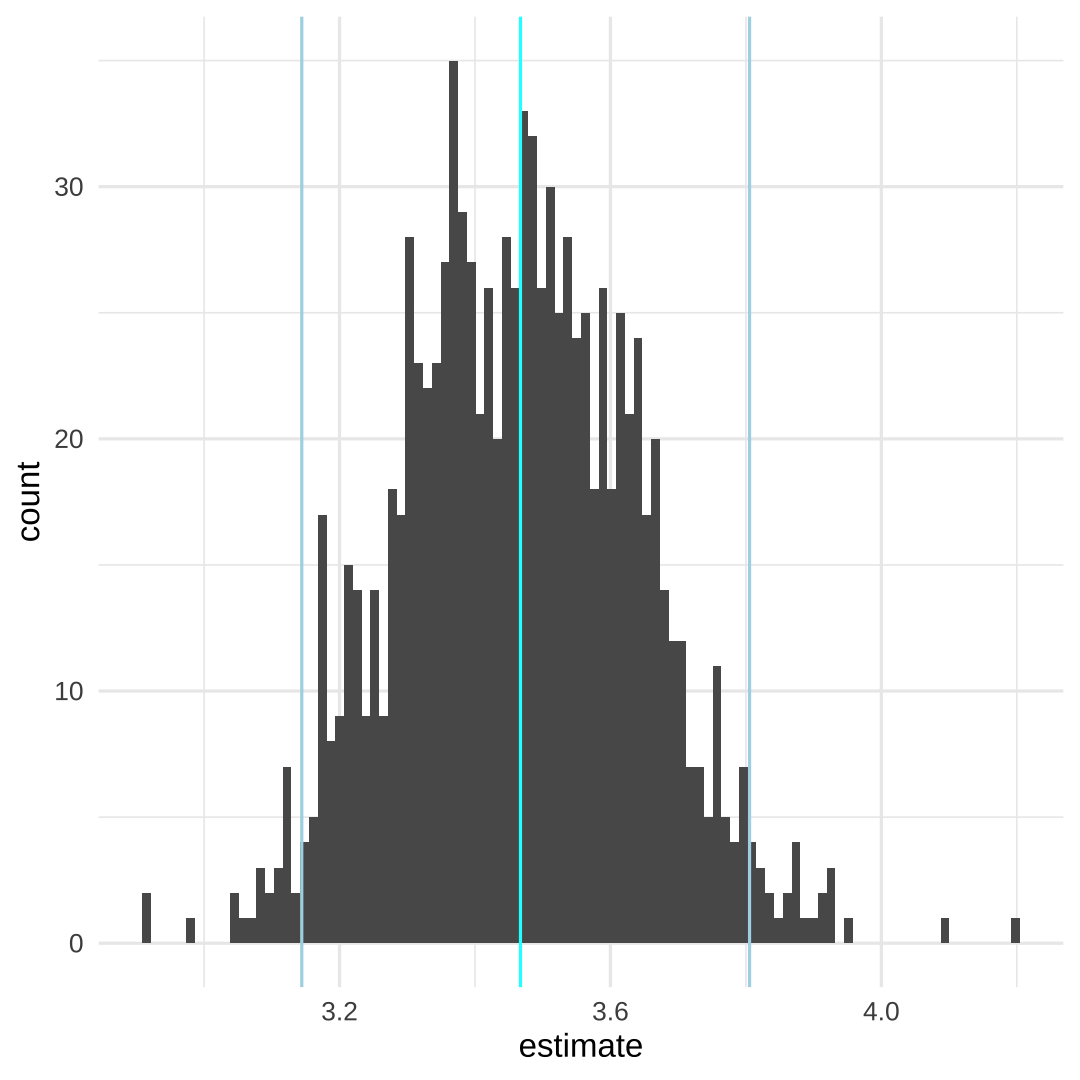
13 / 17
pct_res %>% summarise( Q2.5 = quantile(estimate, probs = 0.025), Q50 = quantile(estimate, probs = 0.5), Q95.7 = quantile(estimate, probs = 0.975) )## # A tibble: 1 x 3## Q2.5 Q50 Q95.7## <dbl> <dbl> <dbl>## 1 3.14 3.47 3.81# M. Hernan: 3.5 (2.6-4.5)14 / 17
13.4 IP weighting or standardization?
- Better precision
- More flexible
- Allows for detailed mediation and interaction analyses
- Both IPTW and coputation of g-formula can be misspecidied
- Doubly robust methods
15 / 17
13.5 How seriously do we take our estimates?
- Identifiability conditions
- Measurement bias
- Selection bias
- Model misspecifications
- Keep calm and remain skeptical 🤓
16 / 17
References
Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC (v. 30mar21)
17 / 17